散度

散度是一个标量，用于体现矢量场各点发散的强弱程度。对于矢量场${ \textbf{F}}$：

${\color{DarkRed} div \textbf{F} = \displaystyle \lim{ \Delta V \to 0}\tfrac{\oint{S} \textbf{F}\cdot d\textbf{S}}{\Delta V} = \nabla \, \cdot \, \textbf{F}}$

${ div \textbf{F}}$描述通量源的密度。

散度定理（高斯定理）：

${\color{Red} \int{V}\nabla\,\cdot \,\textbf{F}dV = \oint{S}\textbf{F}\,\cdot \,d\textbf{S}}$

旋度

散度是一个矢量，用于体现矢量场各点附近环流的强弱程度。对于矢量场${ \textbf{F}}$：

${\color{DarkRed} rot \textbf {F} = \displaystyle \lim{ \Delta S \to 0}\tfrac{1}{\Delta S}\oint{S} \textbf{F}\cdot d\textbf{l}\mathrel{|_{max}} = \nabla \, \times \, \textbf{F}}$

${ rot \textbf{F}}$描述旋涡源的密度。

斯托克斯定理：

${\color{Red}\int{S}\nabla\,\times \,\textbf{F}d\textbf{S} = \oint{C}\textbf{F}\,\times \,d\textbf{l}}$

$\nabla$ Nabla算子

含义：三维直角坐标系中，

$\nabla f=\left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\right)=\mathbf{i}\frac{\partial f}{\partial x}+\mathbf j\frac{\partial f}{\partial y}+\mathbf k\frac{\partial f}{\partial z}$

其中，$\mathbf i， \mathbf j ，\mathbf k$ 依次是 x 、 y 、 z 方向的单位矢量（算子含义与坐标系选取无关，仅列出在三维直角坐标系中的表达式）。

各种意义：

  1. 作用于标量场 $u$ 得到梯度 $\textbf{grad}\, u=\nabla u$;

  2. 与矢量函数点乘得散度：$div\textbf{F} = \nabla \, \cdot \, \textbf{F}$;

  3. 与矢量函数叉乘得旋度：$rot\textbf{F} = \nabla \, \times \, \textbf{F}$;

感性理解为什么求散度用点乘，求旋度用叉乘（看3b1b的www）：

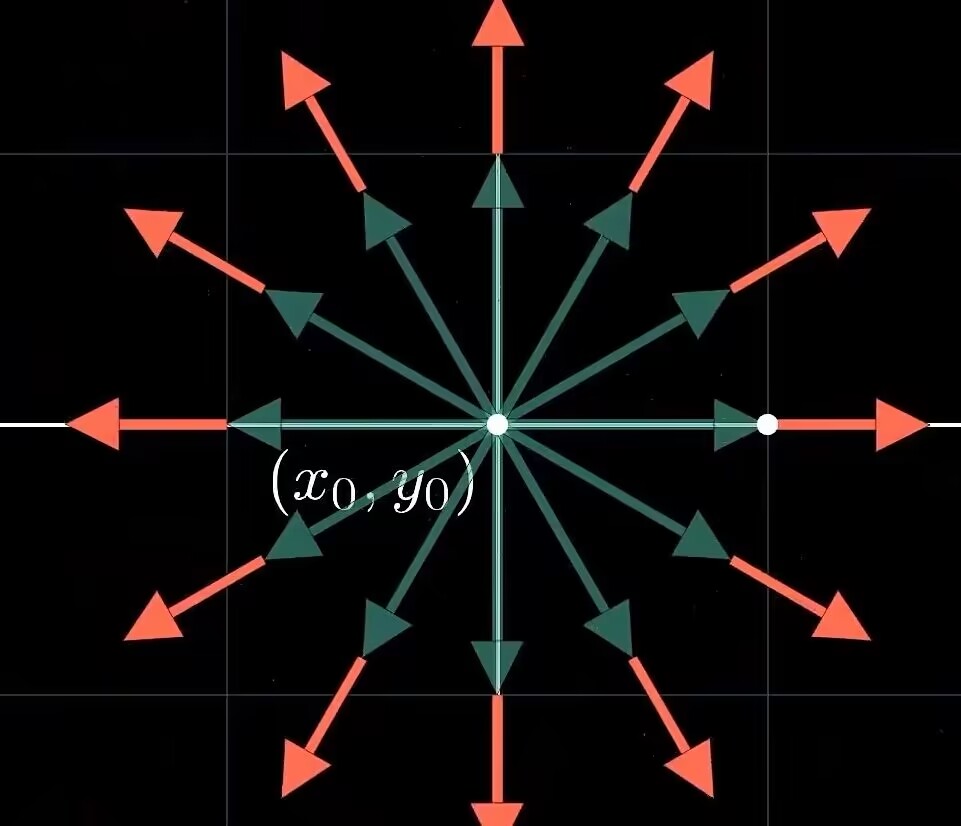
点乘可以衡量两个向量的共线程度，此处即是衡量位移向量和场向量的共线程度（如图对于正通量源点蓝绿色是场向量，红色是位移向量）；

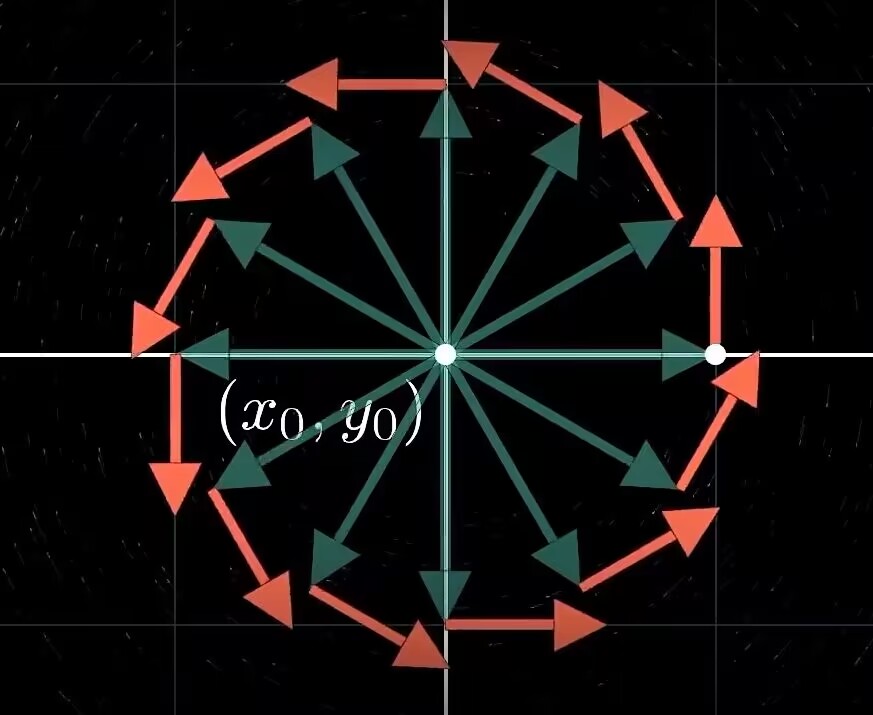
在这里插入图片描述

叉乘可以衡量两个向量的垂直程度，此处即是衡量位移向量和场向量的垂直程度；
在这里插入图片描述

重要定理

格林定理：描述两个标量场之间满足的关系，如果其中已知其中一个场的分布，可以用格林定理求解另一个场的分布。
在这里插入图片描述

亥姆霍兹定理：
在任何有限区域V内，任一矢量场由它的散度、旋度和边界条件惟一地确定。